이번 글은 Explicit Generative model 중 가장 대표적인 Variational Auto-Encoder에 대해 공부한 내용을 정리하려고 합니다.
Explicit model은 Implicit model에 비해 성능이 떨어지지만 저희가 알고 있는 분포를 기반으로 모델링이 되기 때문에 데이터와 결과에 대한 분석이 더 용이하여 사용될 수 있다고 합니다.
Implicit model인 GAN에 비해서 정확히 어떤 식으로 활용되는지는 솔직히 아직 잘 모르겠네요.. 그러나 머신 러닝을 한다면 VAE 정도는 알고 있어야 하지 않을까 싶은 마음에 자세하게 공부를 하게 되었고, 공부한 내용을 정리하는 글을 쓰고자 합니다.
본 글은 "An Introduction to Variational Autoencoders"라는 제목을 가진 paper와 카이스트 문일철 교수님의 강의를 매우 참조하였으며, 보다 자세한 내용은 논문을 참조하시거나 유튜브 AAILab Kaist나 KMOOC-kaist에 있는 강의를 보시길 바랍니다.
그럼 이제 시작.
0. Introduction
아래는 VAE에 대한 기본적인 구조입니다.

VAE는 새로운 데이터 \(\hat{x}\)을 생성하는 model(=decoder)을 만들어내는 것이 목적이라고 할 수 있습니다.
\(\hat{x}\)은 일반적으로 z라는 표기를 붙인 latent vector를 통해 만들어지게 됩니다.
새로운 데이터 \(\hat{x}\)을 잘 만드는 decoder를 만들기 위해선 z를 조절할 필요가 있고, 그 방법은 x라는 데이터를 input으로 받는 encoder를 사용하게 됩니다.
이렇게 encoder, decoder라는 2개의 neural network로 구성된 모델이 VAE입니다.
1. 개요
머신러닝은 임의의 데이터 x를 \(\theta\)라는 파라미터들을 가진 모델을 통과시켜서 특정한 값을 만드는 방법입니다.
그리고 이렇게 나온 특정 값들을 실제 데이터에 근사하도록 \(\theta\)를 학습하는 것입니다.
$$ \mathbf{x} \sim p_{\theta}(\mathbf{x}) $$
$$ p_{\theta}(\mathbf{x})\approx p^{*}(\mathbf{x}) $$
(물론 supervised learning인 경우엔 \(p_{\theta}(\mathbf{y|x}\))를 근사 시킵니다.)
예컨대 MNIST data를 사용한다면, 저희가 학습할 모델은 최대한 MNIST에 나와있는 손글씨 숫자들의 이미지와 비슷한 이미지를 만드는 모델이 되도록 학습을 해야 합니다.
Variational Autoencoder는 neural network(이하 NN)를 사용하기 때문에 \(\theta\)는 NN의 weight와 bias가 되며, 이를 stochastic gradient descent 방법으로 parameter(\(\theta\))를 학습을 하게 됩니다.
VAE는 이러한 기본 구조에 latent variables(\(\mathbf{z}\))를 추가하여 학습을 하는 directed graphical model 입니다. (variational inference)
x 분포에 임의의 z를 marginalized out하여 marginal distribution을 정의할 수 있습니다.
$$ p_{\theta}(\mathbf{x}) \sim \int p_{\theta}(\mathbf{x,z})d\mathbf{z} $$
이때 \(\mathbf{z}\)가 discrete하고 \(p_{\theta}(\mathbf{x|z})\)가 Gassian distribution이라면 marginal distribution \(p_{\theta}(\mathbf{x})\)는 Gaussian Mixture Model과 같은 형태입니다.
또 z가 continuous하다면 \(p_{\theta}(\mathbf{x})\)는 무한개의 분포를 결합시킨 분포가 될 수 있습니다.
이러한 구조를 Deep Latent Variable Model(DLVM)이라 부르기도 하며 DLVM은 간단한 prior, conditional distribution을 가지고도 상당히 정교한 모델을 만들 수 있는 장점이 있습니다.
위의 식에서 간단한 베이즈 룰만 적용하면 새로운 식들을 정의할 수 있습니다.
$$ p_{\theta}(\mathbf{x,z}) = p_{\theta}(\mathbf{z})p_{\theta}(\mathbf{x|z}) $$
$$ p_{\theta}(\mathbf{z|x}) = \frac{p_{\theta}(\mathbf{x,z})}{p_{\theta}(\mathbf{x})} $$
\(p_{\theta}(\mathbf{z})\)는 저희가 직접 정의할 수 있고, 이에 따라 \(p_{\theta}(\mathbf{x|z})\)와 \(p_{\theta}(\mathbf{x,z})\)는 계산이 가능합니다. 하지만 \(p_{\theta}(\mathbf{z|x})\)는 방향이 반대가 되기 때문에 계산하기가 상당히 어렵게 됩니다. 이를 해결하기 위해 variational inference 방법을 사용하게 되고, 그 결과로 encoder 부분이 나타나게 됩니다.
2. Evidence Lower Bound(ELBO)
VAE의 object function도 MLE를 통해 시작됩니다.
latent vector를 가진 MLE는 보통 ELBO라는 하한 값을 maximize하는 차선의 방법을 통해 likelihood를 global optima에 최대한 수렴시키도록 합니다.
일반적으로 ELBO는 Jensen’s inequality를 통해 증명합니다.
이에 대한 설명은 문일철 교수님의 (기계학습, 인공지능, 머신러닝) Explicit DGM-04 | Detour: Evidence LowerBound - YouTube 강의를 보시면 정말 잘 설명되어 있습니다. (이 강의 말고 GMM이나 Variational Inference에서도 계속해서 다루십니다.)
저는 Jensen's inequality보다 더 간단하게 "An Introduction to Variational Autoencoders"에서 제시하는 방법을 이용하겠습니다.

여기서 \(q_{\phi}(\mathbf{z|x})\)는 \(p_{\theta}(\mathbf{z|x})\)를 구하기 위해 만든 recognition model이며 encoder라고도 불립니다.
(2.8) 식을 ELBO를 왼쪽으로 옮겨서 정리하면 다음과 같습니다.
$$ \mathcal{L}_{\theta, \phi}(\mathbf{x}) = \log p_{\theta}(\mathbf{x}) - D_{KL}(q_{\phi}(\mathbf{z|x}) || p_{\theta}(\mathbf{z|x})) $$
이때 \(q_{\phi}(\mathbf{z|x}) \approx p_{\theta}(\mathbf{z|x})\) 되게 만들면 KL Divergence가 0으로 수렴하게 되어 ELBO 값이 오르게 됩니다.
따라서 다음과 같이 됩니다.
$$ \mathcal{L}_{\theta, \phi}(\mathbf{x}) = \log p_{\theta}(\mathbf{x}) - D_{KL}(q_{\phi}(\mathbf{z|x}) || p_{\theta}(\mathbf{z|x})) \leq \log p_{\theta}(\mathbf{x})$$
여기서 ELBO를 올리기 위한 방법은 두가지가 됩니다.
1. Maximize \(\log p_{\theta}(\mathbf{x})\) : decoder의 성능 향상
2. Minimize \(D_{KL}(q_{\phi}(\mathbf{z|x}) || p_{\theta}(\mathbf{z|x}))\) : encoder의 성능 향상
3. Reparameterization Trick
Reparameterization Trick에 대한 설명도 첫 VAE 논문인 "Auto-Encoding Variational Bayes"에선 다른 방법으로 표현합니다. 저는 역시나 "An Introduction to Variational Autoencoders"에서 나오는 간단한 방법을 소개하고자 합니다.
(2.8)을 보시면 ELBO에 대한 정의가 있습니다.
$$ ELBO : \mathcal{L}_{\theta, \phi}(\mathbf{x}) = \mathbb{E}_{q_{\phi}(\mathbf{z|x})}[\log p_{\theta}(\mathbf{x|z}) - \log q_{\phi}(\mathbf{z|x})] $$
저희가 미분해야 할 파라미터는 \(\theta\), \(\phi\) 입니다.
먼저 \(\theta\)에 대한 미분은 다음과 같이 가능합니다.

\(\theta\)는 (2.17) 식으로 Monte Carlo sampling을 통하여 학습이 가능합니다.
그러나 문제는 variational parameter인 \(\phi\)입니다.
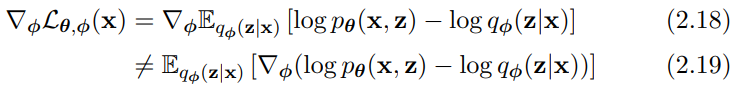
Expectation 안에 미분이 들어간 형태가 되어야 Monte Carlo sampling으로 학습이 가능한 형태가 됩니다.
하지만 현재의 z는 random variable이기 때문에 backpropagation이 불가능한 상태입니다.
위의 \(\mathbf{z}\)를 monte carlo sampling으로 풀어보면 아래와 같은 형태가 됩니다.

\(f(\mathbf{z})\)가 미분이 불가능한 형태죠.
위처럼 sampling 된 \(\mathbf{z^{\mathit{l}}} \sim q_{\phi}(\mathbf{z|x^{\mathit{i}}})\) 는 variance도 매우 크기 때문에 optimize 하기에 적합하지 않다고도 하네요.
따라서 Reparameterization Trick이란 방법으로 noise(\(\epsilon\))를 추가하여 \(\epsilon\)을 기준으로 미분하는 방법을 선택하게 됩니다.

아이디어는 \(q_{\phi}(\mathbf{z|x^{\mathit{i}}})\)를 만드는 과정에서 noise(\(\epsilon\))를 추가하는 것입니다.
그리고 \(\epsilon\)을 통해 Backpropagation이 가능하도록 z의 형태를 deterministic하게 바꾸는 것입니다.
결과적으로 z가 저희가 원하는 방향으로 바뀌면 되는 것이니까요.
(물론 이 때 \(\epsilon\)을 추가하는 함수는 당연히 역변환이 가능해야 합니다.)
이렇게 함으로써 임의의 sample인 \(q_{\phi}(\mathbf{z^{\mathit{l}}|x^{\mathit{i}}})\)를 뽑아도 \(\mathbf{z^{\mathit{l}}}\)는 우리가 특정한 \(\mu\), \(\sigma\)의 값으로 구성된 deterministic variable이 됩니다.
reparameterization trick을 적용시킨 뒤 수식은 아래처럼 변하여 전체가 미분이 가능해지며 monte carlo sampling이 가능해집니다.
$$ \mathbf{z} = \mathbf{g}(\phi, \epsilon, x) \;\mathrm{with}\; \epsilon \sim p(\epsilon) $$
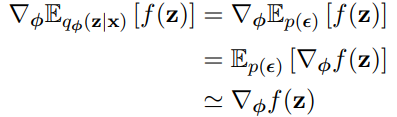
그렇다면 \(\mathbf{z}\)에 \(\epsilon\)을 추가하는 함수 \(\mathbf{g}\)는 어떻게 구성되어 있을까요?
가장 일반적인 예시는 역시 Gaussian Distribution 입니다.

위와 같이 분산에 epsilon을 곱하여 새로운 z를 샘플링하게 됩니다.
encoder를 통과하여 평균과 표준편차 값이 나오게 되고, epsilon으로 미분하여 \(\phi\)를 업데이트해나갑니다.
물론 decoder에는 encoder에서 나온 평균과 표준편차로 새롭게 sampling 된 z가 들어갑니다.
(여기서 \(\sigma\)는 diagonal 부분만을 의미하지만 \(\sum\)과 같이 full matrix를 다 사용하는 방법도 있습니다.
자세한 건 논문으로..)
이렇게 해서 Backpropagation이 가능해지고 모델 학습이 가능해지게 됩니다.
4. 정리
(1) 우리가 알고 싶은 것은 \(p_{\theta}(\mathbf{x})\)가 최대값이 되도록 만드는 \(\theta\)
(2) 이를 위해 marginal distribution을 근사화시키는 방법을 사용한다. 이는 Decoder(혹은 generative model)
$$ p_{\theta}(\mathbf{x}) \sim \int p_{\theta}(\mathbf{x,z})d\mathbf{z} $$
(3) marginal likelihood를 최대화하기 위해 variational parameter를 만들고, 이는 Encoder (혹은 recognition model)이 된다.
= \( q_{\phi}(\mathbf{z|x}) \)
(4) latent vector를 미분 가능하게 sampling 하기 위해서 reparameterization trick을 사용한다.(\(\epsilon\) 추가)
(5) 최종 Loss function은 아래가 된다. (1번째 텀은 KL Divergence, 2번째 텀은 Reconstruct Error)
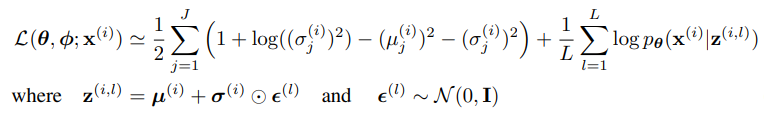
(6) 학습!
(7) 학습이 끝나면 random variable을 받으면 이미지를 생성하는 decoder를 얻을 수 있다.
5. 코드
코드 : https://github.com/nhm0819/GAN_prac/blob/main/VAE.ipynb
참조 : https://github.com/lyeoni/pytorch-mnist-VAE
MNIST dataset 기준으론 z의 차원이 2차원인 경우가 가장 잘 학습된다고 합니다.
latent vector의 차원을 마구 늘린다고 해서 꼭 좋은 것은 아닌가 보네요.

z 값에 따라 어떤 특징들이 변화시킨다는 걸 알 수 있습니다.
한눈에 봐도 얼추 규칙적이라는 느낌이 들죠..?
이러한 특징을 파악할 수 있다는 것이 explicit model의 장점인 것 같습니다.
결과적으로 성능은 물론 GAN이 좋지만요.
시간이 난다면 좀 더 심화된 VAE 종류들도 공부해보면 좋을 것 같습니다.
'ML theory' 카테고리의 다른 글
| Optimzer 정리 (0) | 2022.03.31 |
|---|