Optimzer 정리
헷갈리면 들어와서 볼 수 있도록 정리한 글.
1. Stochastic Gradient Descent


Gradient Descent 방법을 mini batch 단위로 적용시키는 방법.
가장 기본 방법.
2. Momentum

이전에 적용했던 gradient 값도 반영시키는 방법.
\(v_{t}\)는 적용될 gradient의 크기 혹은 속도로 표현됨.
3. Adagrad
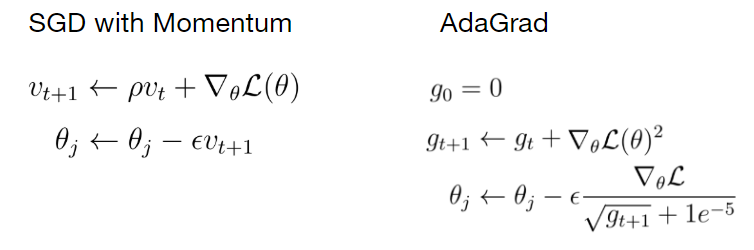
gradient의 제곱을 이용하여 학습 방향을 조정.
(다른 곳에선 \(h\)로 표기하는데 식을 가져온 사이트에선 \(g\)로 표기했다.)
이 때 제곱은 각 요소들의 제곱으로 사실은 저런 표현은 헷갈리는 표현이다.
$$ \bigtriangledown_{\theta}\mathcal{L}(\theta)^{2} = \bigtriangledown_{\theta}\mathcal{L}(\theta)\bigodot \bigtriangledown_{\theta}\mathcal{L}(\theta) $$
다음과 같이 일반 행렬 곱셈이 아니라, hadamard product를 통해서 같은 위치의 요소들이 각각 곱해지는 방식이다.
따라서 \(\bigtriangledown_{\theta}\mathcal{L}(\theta)^{2}\)은 \(\bigtriangledown_{\theta}\mathcal{L}(\theta)\)과 같은 shape을 가진 matrix 형태가 된다.
그리고 이의 역수를 나눠줌으로써 각 gradient 마다 크기가 큰 gradient는 조금만 업데이트되고, 크기가 작은 gradient는 더 많이 업데이트 되는 방법이다.
4. RMSprop

\(g_{t+1}\)을 조절할 때 이전의 \(g_{t}\)를 반영한다.
5. Adam
\(v_{t+1}\)과 \(g_{t+1}\), 둘 다 moving average를 반영하는 기법.
또한 초기값을 0으로 두면서 0으로 편향(bias)되는 문제를 해결하기 위해 bias-corrected 방법을 추가함.
